Equal Products and Equal Sums of Like Powers

`Equal Sums of Like Powers`

Equal Products and Equal Sums of Like Powers

a₁a₂ ... a_m = b₁ b₂ ... b_m

a₁^k + a₂^k + ... + a_m^k = b₁^k + b₂^k + ... + b_m^k ( k = k₂ , k₃, ... , k_n )

Introduction
Why use k = 0 for the equal products equation?
General theorems
Ideal non-negative integer solutions
Ideal integer solutions

Introduction

The Equal Products and Equal Sums of Like Powers is the system of the form

a₁a₂ ... a_m = b₁ b₂ ... b_m

a₁^k + a₂^k + ... + a_m^k = b₁^k + b₂^k + ... + b_m^k ( k = k₂ , k₃ , ... , k_n )

This system has been studied for a long time when k <= 3.[13] [5] [17] [6] [59]

In March of 2001, for the first time, Guo Xianqiang and Chen Shuwen found that the equal products equation can be regarded as the k = 0 case of the Equal Sums of Like Powers system.

In these pages, we will denote the Equal Products and Equal Sums of Like Powers system as:

[ a₁ , a₂ , ... , a_m ] = [ b₁ ,b₂ , ... , b_m ] ( k = 0, k₂ , k₃ , ... , k_n )

Why use k = 0 for the equal products equation?

The following explanation is given by Guo Xianqiang:

A similar expression are available on a web site about General Mean.

So both the equal products equation and the equal sums of like powers system can be expressed as S_r( A ) = S_r( B ):

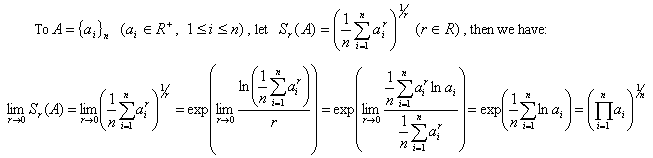
a₁a₂ ... a_m = b₁ b₂ ... b_m <=> S₀( A ) = S₀( B )

a₁^k + a₂^k + ... + a_m^k = b₁^k + b₂^k + ... + b_m^k <=> S_k( A ) = S_k( B )

We may also consider the graph of the following function to see more clearly:

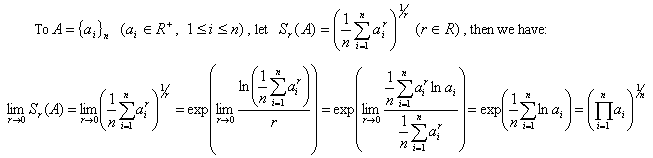
y = { ( a₁^x+a₂^x+a₃^x+a₄^x+a₅^x ) / 5 }^1/x - { ( b₁^x+b₂^x+b₃^x+b₄^x+b₅^x ) / 5 }^1/x

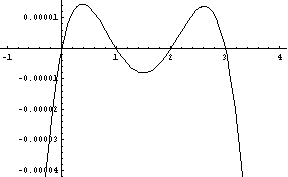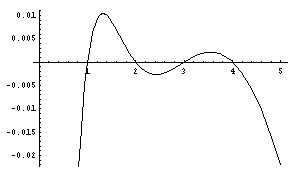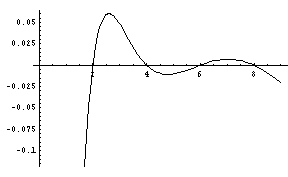{ a_i } = { 54, 60, 63, 77, 80 } { b_i } = { 56, 56, 66, 75, 81 } [ a_i ] = [ b_i ] ( k = 0, 1, 2, 3 )	{ a_i } = { 1, 5, 9, 17, 18 } { b_i } = { 2, 3, 11, 15, 19 } [ a_i ] = [ b_i ] ( k = 1, 2, 3, 4 )
{ a_i } = { 1, 8, 13, 24, 27 } { b_i } = { 3, 4, 17, 21, 28 } [ a_i ] = [ b_i ] ( k = 1, 2, 3, 5 )	{ a_i } = { 7, 18, 55, 69, 81 } { b_i } = { 9, 15, 61, 63, 82 } [ a_i ] = [ b_i ] ( k = 1, 2, 3, 6 )
{ a_i } = { 3, 7, 10, 16, 16 } { b_i } = { 4, 5, 12, 14, 17 } [ a_i ] = [ b_i ] ( k = 1, 2, 4, 6 )	{ a_i } = { 3, 19, 37, 51, 53 } { b_i } = { 9, 11, 43, 45, 55 } [ a_i ] = [ b_i ] ( k = 1, 3, 5, 7 )
{ a_i } = { 71, 131, 180, 307, 308 } { b_i } = { 99, 100, 188, 301, 313 } [ a_i ] = [ b_i ] ( k = 2, 4, 6, 8 )	( Ploted by Mathematica, Chen Shuwen )

The Equal Products and Equal Sums of Like Powers System which we denote here as ( k = 0, k₂ , ... , k_n ) has the same properties as the normal Equal Sums of Like Powers System ( k = k₁, k₂ , ... , k_n ). For example:

Non-negative integer solutions are available only when m>=n+1.
Integer solutions are available only when m>=n.
Both satisfy the following relation ( See also Conjectures by Chen Shuwen ) when m=n+1:

0 <= a₁ < b₁ <= b₂ < a₂ <= a₃ < b₃ <= b₄ < a₄<= ... ( assume a₁ < b₁)

General theorems

Theorem 7 (By Chen Shuwen)

[ a₁ , a₂ , ... , a_n ] = [ b₁ , b₂ , ... , b_n ]

( k = 1, 2, ... , n-2, n )

Then

[ Sa₁ + T , Sa₂ + T , ..., Sa_n + T ] = [ Sb₁ + T , Sb₂ + T , ... , Sb_n + T ]

( k = 0, 1, 2, ... , n-2 )

where T = , S = .

Theorem 8 (By Quo XianQiang)

[ a₁ , a₂ , ... , a_m ] = [ b₁ , b₂ , ... , b_m ]

( k = k₁, k₂ , ... , k_n )

then

[ a₁ , a₂ , ... , a_m , Tb₁ , Tb₂ , ... , Tb_m ] = [ b₁ , b₂ , ... , b_m , Ta₁ , Ta₂ , ... , Ta_m ]

( k = 0, k₁, k₂ , ... , k_n )

where T is arbitrary integer.

Ideal non-negative integer solutions

It seems that there is no non-negative integer solutions when m=n. Here we consider the m=n+1 case:

a₁a₂ ... a_n₊₁ = b₁ b₂ ... b_n₊₁

a₁^k + a₂^k + ... + a_n₊₁^k = b₁^k + b₂^k + ... + b_n₊₁^k ( k = k₂ , ... , k_n )

This system will be denoted as:

[ a₁ , a₂ , ... , a_n₊₁ ] = [ b₁ ,b₂ , ... , b_n₊₁ ] ( k = 0, k₂ , ... , k_n )

When k₁= 0 and all others k> 0, idea non-negative integer solutions have been found to the following 24 types:

( k = 0 )

[ 1, 6 ] = [ 2, 3 ]
[ 1, 24 ] = [ 2, 12 ] = [ 3, 8 ] = [ 4, 6 ]

( k = 0, 1 )

[ 4, 15, 15 ] = [ 5, 9, 20 ]

By A.Moessner in 1939.[13]

[ 2, 12, 15 ] = [ 3, 6, 20 ]

By A.Golden in 1944.[5]

( k = 0, 2 )

[ 13, 38, 51 ] = [ 17, 26, 57 ]

This type goes back at least to Bini, with partial solutions by Dubouis and Mathieu.[49]
By G.Xeroudakes and A.Moessner in 1958.[17]

[ 15, 42, 48 ] = [ 16, 35, 54 ] = [ 21, 24, 60 ]

By T.N.Sinha in 1984.[6]

( k = 0, 3 )

[ 1, 108, 120 ] = [ 9, 10, 144 ]

Stephane Vandemergel has found 62 solutions at least before 1994.[49]
By Chen Shuwen in 2001.

( k = 0, 4 )

[ 22, 93, 116 ] = [ 29, 66, 124 ]

Stephane Vandemergel has found 3 solutions at least before 1994.[49]
Found independently by Chen Shuwen in 2001.

[ 3481, 21014, 21172 ] = [ 7847, 7906, 24964 ]

By Chen Shuwen in 2001.

( k = 0, 1, 2 )

[ 2, 2, 11, 21 ] = [ 1, 6, 7, 22 ]

By A.Golden in 1944.[5]

[ 3, 14, 20, 40 ] = [ 4, 8, 30, 35 ]

By G.Xeroudakes and A.Moessner in 1958.[17]

( k = 0, 1, 3 )

[ 5, 11, 16, 24 ] = [ 6, 8, 20, 22 ]

First known solution, by Chen Shuwen in 2001.

( k = 0, 1, 4 )

[ 7, 18, 60, 80 ] = [ 5, 36, 40, 84 ]
- There are only 1 solution in the range of max{a_i,b_i}<=150, by Chen Shuwen in 2017.

( k = 0, 1, 5 )

[ 21, 31, 130, 143 ] = [ 13, 66, 91, 155 ]
[ 91, 129, 196, 299 ] = [ 84, 161, 169, 301 ]
- There are only 2 solutions in the range of max{a_i,b_i}<=305, by Chen Shuwen in 2017.

( k = 0, 2, 3 )

[ 855, 4338, 10406, 16335 ] = [ 1215, 2838, 11495, 15906 ]

First known solution, by Chen Shuwen in 2022.

( k = 0, 2, 4 )

[ 19, 67, 159, 207 ] = [ 23, 53, 171, 201 ]

First known solution, by Chen Shuwen in 2001.

( k = 0, 2, 6 )

[ 155, 779, 1455, 1887 ] = [ 185, 615, 1581, 1843 ]

First known solution, by Chen Shuwen in 2017-05-19.

( k = 0, 1, 2, 3 )

[ 4, 13, 17, 40, 50 ] = [ 5, 8, 25, 34, 52 ]

First known solution, by Guo Xianqiang in 2000.

[ 54, 60, 63, 77, 80 ] = [ 56, 56, 66, 75, 81 ]

By Chen Shuwen in 2001.

( k = 0, 1, 2, 4 )

[ 4, 4, 15, 15, 22 ] = [ 3, 6, 11, 20, 20 ]
[ 8, 9, 18, 21, 28 ] = [ 7, 12, 14, 24, 27 ]
- There are 21 solutions in the range of max{a_i,b_i}<=96, by Chen Shuwen in 2017.

( k = 0, 1, 2, 6 )

[ 205, 248, 255, 344, 351 ] = [ 215, 221, 279, 328, 360 ]
- First known solution, by Chen Shuwen in 2017-05-31.

( k = 0, 2, 4, 6 )

[ 2, 16, 25, 45, 48 ] = [ 3, 9, 32, 40, 50 ]
[ 8, 33, 38, 68, 87 ] = [ 12, 17, 57, 58, 88 ]

There are 10 solutions in the range of max{a_i,b_i}<=150, by Chen Shuwen in 2017.

( k = 0, 1, 2, 3, 4 )

[ 169, 175, 192, 215, 216, 228 ] = [ 171, 172, 195, 208, 224, 225 ]

First known solution, by Chen Shuwen in 2001.

( k = 0, 1, 2, 3, 5 )

[ 28, 57, 100, 174, 200, 245 ] = [ 30, 49, 125, 140, 228, 232 ]

First known solution, by Chen Shuwen in 2017-04-15.

( k = 0, 1, 2, 4, 6 )

[ 5, 12, 15, 32, 36, 46 ] = [ 6, 8, 23, 24, 40, 45 ]
[ 8, 16, 24, 45, 55, 66 ] = [ 10, 11, 33, 36, 60, 64 ]

There are 4 solutions in the range of max{a_i,b_i}<=100, by Chen Shuwen in 2017.

( k = 0, 1, 2, 3, 4, 5 )

[ 480, 497, 558, 595, 616, 663, 666 ] = [ 481, 495, 568, 578, 630, 651, 672 ]

First known solution, by Chen Shuwen in 2001.

( k = 0, 1, 2, 3, 4, 6 )

[ 32, 40, 41, 69, 72, 88, 90 ] = [ 33, 36, 45, 64, 80, 82, 92 ]
[ 14, 33, 37, 108, 112, 192, 221 ] = [ 17, 21, 52, 88, 128, 189, 222 ]

First known solution, by Chen Shuwen in 2017-05-26.

( k = 0, 1, 2, 4, 6, 8 )

[ 437, 497, 732, 754, 1034, 1107, 1233 ] = [ 423, 548, 621, 902, 923, 1159, 1218 ]
- First known solution, by Chen Shuwen in 2023-02-12.

( k = 0, 1, 2, 3, 4, 5, 6 )

[ 1899, 1953, 1957, 2079, 2117, 2231, 2241, 2323 ] = [ 1909, 1919, 2001, 2037, 2163, 2187, 2263, 2321 ]

First known solution, by Chen Shuwen in 2001.

[ 11, 19, 22, 54, 60, 90, 92, 111 ] = [ 12, 15, 27, 46, 74, 76, 99, 110 ]
[ 7, 15, 21, 50, 53, 88, 96, 110 ] = [ 8, 11, 32, 33, 70, 75, 105, 106 ]
- Smallest solution, by Chen Shuwen in 2017.

( k = 0, 1, 2, 3, 4, 5, 6, 7 )
- [ 387, 388, 416, 447, 494, 536, 573, 589, 610 ] = [ 382, 402, 403, 456, 485, 549, 559, 596, 608 ]
  - First known solution, by Chen Shuwen in 2023-04-08.

Ideal integer solutions

Integer solutions have been found to the m=n case:

a₁a₂ ... a_n = b₁ b₂ ... b_n

a₁^h + a₂^h + ... + a_n^h = b₁^h + b₂^h + ... + b_n^h ( h = h₂ , ... , h_n )

Also, this system will be denoted as:

[ a₁ , a₂ , ... , a_n ] = [ b₁ ,b₂ , ... , b_n ] ( h = 0, h₂ , ... , h_n )

When h₁= 0 and all others h> 0, idea integer solutions have been found to the following 6 types:

( h = 0, 1, 3 )

[ -15, 1, 14] = [ -10, 3, 7 ]

By A.Moessner in 1939. [13]

( h = 0, 1, 2, 4 )
- [ -138, 9, 62, 67 ] = [ -93, -23, -18, 134 ]
  - By Ajai Choudhry in 2011. [1301]
( h = 0, 1, 3, 5 )
- [ -260, 32, 189, 323 ] = [ -210, 68, 114, 312 ]
- [ -555, -21, 646, 650 ] = [ -255, -78, 350, 703 ]
  - By Chen Shuwen in 2017-03-26.
- [ -1518, 14, 1363, 1581 ] = [ -561, 138, 406, 1457 ]
  - By Chen Shuwen in 2023-04-24.
( h = 0, 1, 2, 3, 5 )
- [ -21, -20, 2, 13, 26 ] = [ -26, -13, 5, 6, 28 ]
  - By Ajai Choudhry in 2011. [1301]
( h = 0, 1, 2, 4, 6 )
- [ -48, -2, 16, 25, 45 ] = [ -40, -9, 3, 32, 50 ]
  - By Chen Shuwen in 2017-03-21.
( h = 0, 1, 2, 3, 4, 6 )
- [ -11716, -6437, -1460, 1175, 7897, 10541 ] = [ -10865, -8383, -596, 3683, 4700, 11461 ]
  - By Ajai Choudhry in 2011. [1301]